Analysis of the contact layer of the running edge of the straight toothed gear
Heat Treated Steel Bar And Tube
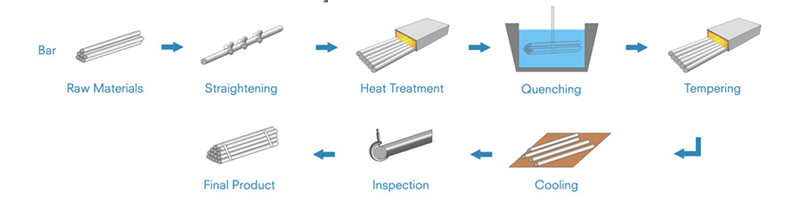
HEAT TREATED STEEL BAR AND TUBE
Heat treated steel bar is produced by heating and cooling in different temperature based on the steel grades to improve the steel bar mechanical properties or machinability for various industrial applications. Heat treated steel bar includes annealed steel bars, Normalized Steel Bar, quenched and temper qt steel bar.
Annealed Steel Bar has better ductility and lower hardness, which can be easier to be machined. The annealing processing is usually widely used for steel grade with higher carbon content above 0.5%. However, some low carbon steel also requires to do annealing for special usage such as 20CrMnTi gear steel. For some special material such as 20CrMnTi gear steel and GCr15 such bearing steel, spheroidizing annealing is often required.
Normalized steel bar sometime is also one kind of annealing processing. It mainly changes the grain to remove the impurities in steel and improves the strength and hardness. For some hot rolled steel bars, to keep the basic mechanical properties, normalizing is often used.
Quenching and Tempering, abbreviated as Q&T is a king of processing that strengthen or harden steel bars by heating the materials and then cooling in water, oil or other liquid medium, that rapidly the change from austenite to perlite to get the proper properties for various usage. The quenched & tempered steel bar materials are usually with carbon from 0.30% - 0.60%, it is widely used as merchant bars in components of various machines.
Our advantages on producing heat treated steel bars:
1) Big stocks of hot rolled round bars or wire rods as raw materials
2) Wide range of Cold Drawn Steel Bar sizes: from 10mm to 150mm
3) Different cold drawing medias powder or oil to get different surface
4) Straightening machines to get better straightness up to 0.5mm/m
5) Grinding and polishing machines to get better roughness upto 0.4um
6) Heat treating furnaces to adjust the mechanical properties
7) Full sets of testing equipment to test the sizes, mechanical properties and microstructure.
8) Multiple packages to avoid broken packages and anti-rusty
Astm A193,Round Steel Tubing,Heat Treated Steel Tube,Heat Treated Steel Bar And Tube SHANDONG LE REN SPECIAL STEEL CO., LTD. , https://www.sdbrightsteelbar.com
The face gear transmission is a gear transmission in which a spur gear meshes with a bevel gear. When the two wheel axes are orthogonal, the bevel gear becomes a face gear, which is called a face gear transmission. The edge contact of the face gear transmission is when the gear pair enters the meshing state, the tooth root portion of the spur gear is in contact with the tooth tip edge of the driven face gear, or the tooth root portion of the driven face gear is active when the meshing is exited. The tips of the pinions of the small wheels are in contact. Since the contact path of the spur gear drive is perpendicular to the root cone of the face gear, edge contact is unavoidable when entering or exiting engagement, and it is considered that the loaded gear drive may have a large margin at the edge contact point. Vibration and noise. Therefore, how to effectively avoid edge contact and improve its dynamic performance has always been the goal pursued by the spur gear pair design.
The author first proposes a simple geometric method for solving the contact between the tooth tip edge of the face gear and the small tooth tooth surface. The edge contact point is compared with the closest tooth surface meshing point on the contact surface to determine the edge curvature. Based on the finite element contact analysis method, the nonlinear programming method of the finite element compliance matrix is ​​used to solve the tooth contact problem of the face gear.
One-sided gear transmission tooth contact analysis tooth contact analysis is established as a 1 coordinate system. The coordinate systems S1 and S2 are respectively a moving coordinate system fixed to the spur gear and the face gear, and Sf is a fixed coordinate system. In order to study the meshing characteristics under the condition of installation error, the auxiliary coordinate system Sq, Sd and Se. The positional relationship of each coordinate system is established as shown in Fig. 1. 1: E is the axis staggered displacement error; q is the axial offset error of the face gear pair; f=m, m is the axis intersection angle, which is the axis angle error.
In S1 and S2, the equation of the spur gear tooth surface 1 and the face gear tooth surface 2 and the normal vector can be expressed as r1=r1(u1,1)(1)n1=n1(u1,1)(2)
R2=r2(us,s,s)(3)
N2=n2(us,s,s)(4)
In the coordinate system Sf, the equations and normals of the spur gear and the face gear are r(1)f(u1,1,1)=Mf1(1)r1(u1,1)(5)n(1)f(u1 ,1,1)=Lf1(1)n1(u1,1)(6)r(2)f(u1,s,s,2)=Mf2(2)r2(us,s,s)(7)n (2) f(us, s, s, 2) = Lf2 (2) n2 (us, s, s) (8) where: (u1, 1), (us, s) is the small wheel and the face gear Tooth surface parameters; 1, 2 are the rotation angles of the spur gear and the face gear respectively; Mf1 is the transformation matrix of S1 to Sf; Lf1 is the matrix after Mf1 eliminates the last row and the last column; Mf2=MfqMqdMdeMe2 is the transformation of S2 to Sf The matrix; Lf2 is the matrix after Mf2 eliminates the last row and the last column; s is the corner when the gear shaping tool is used to form a face gear. In the two-wheel meshing, the position vector is necessarily equal to the normal vector, so there are r(1)f(u1,1,1)-r(2)f(us,s,s,2)=0(9)n(1 ) f(u1,1,1)-n(2)f(us,s,s,2)=0(10) Thus, six scalar equations can be obtained. But only 5 of them are independent of each other, because |n(1)f|=|n(2)f|. Consider the meshing equation f2s (us, ls, s) when the gear shaping tool is added to the face gear. =nsv(s2)s=0(11) There are 6 independent equations and 7 unknowns. Let 1 be the input quantity, and the remaining 6 parameters {u1(1), 1(1), us(1), s(1), s(1), 2(1)}C1 can be solved.
The geometrical error function of the face gear pair is defined as 2(1)=(2-02)-N1N2(1-01)(12) where: 02 and 01 are the initial corners of the small spur gear and the face gear; 2 and 1 are The actual rotation angle of the spur gear and the face gear; 2 (1) is the rotation angle of the active spur gear which actually lags the surface gear during the meshing process.
2 Edge contact analysis 21 The small tooth tip edge is in contact with the face gear tooth surface. When the meshing is withdrawn, the tooth tip edge of the small wheel may be in contact with the tooth surface of the face gear. At this time, in the fixed coordinate system Sf, the tip end edge of the small wheel has the same position vector as the tooth surface of the face gear, and the tooth tip edge cut vector of the pinion gear is perpendicular to the tooth surface normal of the face gear. Therefore, there is r(1)fr(2)f=0r(1)f1n(2)f=0f2s(us,s,s)=0r21x r21y-r2a1=0(13) where:r(1)f,r (2) f is the position vector of the two tooth faces respectively; r(1)f/1 is the tangent vector of the top edge of the small gear tooth; n(2)f is the unit normal vector of the tooth surface of the face gear; r1x, r1y, ra1 They are the projection of the small wheel tooth surface vector on the x-axis and the y-axis and the tip circle radius of the small wheel. Taking 1 as an input parameter, the position coordinates on the contact surface of the face gear when the tooth tip edge of the pinion is in contact with the tooth surface of the face gear can be obtained.
Similarly to the contact of the pinion of the face gear of the 22-face gear, the tooth surface of the pinion may come into contact with the tip edge of the face gear when entering the mesh. In the fixed coordinate system Sf, the crest edge of the face gear has the same position vector as the tooth surface of the pinion, and the crest edge cut vector of the face gear is perpendicular to the tooth face normal vector of the pinion. However, since the face gear tooth surface equation is very complicated, it is impossible to determine the tooth tip edge cut vector of the face gear by the partial derivative method. On the basis of the literature [7], the author considers the particularity of the face gear structure, and obtains the tangent vector of the tooth tip edge of the face gear by using the cross product of the face gear tooth head unit method vector and the face gear tooth surface method vector. , such as 2.
The normal vector of the tooth surface of the 2-sided gear tooth is na2=cos-sin0sincos010-sin(m-90)cos(m-90)(14) where: m is the angle of intersection; =arctan(X2/Y2) . It is known from equation (2) that in the S2 coordinate system, the unit normal vector of the face gear is n2, and the tangent vector of the edge curve generated by the intersection of the tooth tip of the face gear and the tooth surface is expressed as T2=na2n2 (15)
Transform the vector into a fixed coordinate system Sf T(2)f=Lf2T2(16)r(1)fr(2)f=0T(2)fn(1)f=0f2s(us,s,s)=0r22x R22z-r2ds = 0 (17) where: r2x, r2z, rds are the projection of the face gear tooth surface vector on the x-axis and the z-axis, respectively, and the root radius of the pinion cutter. Taking 1 as an input parameter, the position coordinates of the pinion contact curved surface when the tooth tip edge of the face gear is in contact with the tooth surface of the pinion can be obtained.
23 The approximate principal curvature direction on the edge contact surface is determined by the relative principal curvature direction of the two tooth surface contact, that is, the long axis direction of the contact ellipse, which is obtained by the contact analysis (TCA) of the tooth when the tooth surface is in contact; When the tooth surface is in contact with the edge of the other tooth surface, there is no exact method to solve the main direction problem of the contact area because the positional relationship between the two contact surfaces is uncertain. When edge contact occurs, how to determine the possible contact direction under load and the possible discrete point information along the direction will have a certain influence on the tooth surface bearing contact analysis (LTCA) of the gear pair.
Professor Fang Zongde et al. studied the edge contact problem between spiral bevel gears and hypoid gears, and proposed a method for generating the main direction in the vicinity of the contact point by numerical method and obtaining the tooth surface clearance at discrete points along the direction. .
In this paper, for the simplification of the problem, it is assumed that in the range of the tooth surface near the edge contact point, the direction of the main curvature coincides with the direction of the main curvature of the tooth surface meshing point closest to the distance, that is, the two tooth faces closest to the distance The meshing point contacts the long axis direction of the ellipse as the main direction of the edge contact curved surface. The distance between the edge contact point and the closest tooth surface contact point is determined by the density of discrete contact points taken on the tooth surface. Thereby, the approximate main curvature direction on the curved surface and the gap information along the direction when the edge contact occurs can be obtained.
3 Bearing contact analysis of edge contact The analysis of edge bearing contact is the same as that of conventional tooth surface. The nonlinear programming is described as min2n 1j=1Xj,-[F][p] [Z] [d] [X]=[w ], (18) P = [e] T [p] X2n 1, s.. tpj0, dj0, Z0, Xj0, (j = 1, 2,, n) pj = 0 or dj = 0 (j = 1, 2,, n) (19) contact state condition, if pj>0, then dj=0(j=1,2,,n)(20) If pj=0, then dj>0 (j=1,2,, n)(21)
Where: Xj(j=1, 2,, 2n 1) is an artificial variable; [F] is a nn-order normal compliance matrix of the pair of teeth (previously solved by the finite element method); [p] is n-dimensional Instantaneous contact with the normal load at the discrete point of the ellipse long axis; [d] is the tooth surface normal gap at the discrete point of the instantaneous contact ellipse long axis after n-dimensional deformation; [w] is the n-dimensional initial tooth surface normal gap , including geometrical transmission error (determined by tooth contact analysis in advance); [Z] is the normal displacement P of the two flank surfaces after n-dimensional deformation is the applied load [X]=[X1,X2,,X2n]T; Each element of the dimension vector [e] is 1.
Solving the above mathematical programming, the normal displacement [Z] after deformation of the tooth tooth, the discrete load [p] at the discrete point of the instantaneous contact ellipse long axis and the tooth surface normal gap at the discrete point after deformation [d] will be obtained. The normal displacement Z after the tooth deformation is converted into an angle value, and the bearing transmission error of the gear pair can be obtained. The load distribution coefficient is obtained from the discrete load p at the discrete point.
1 gear pair design parameters Table 4 analysis example design parameters see 1. Example 1 shaft angle m = 90, no installation error, regardless of edge contact and consider the edge contact surface gear tooth surface imprint, transmission error and For the tooth surface load distribution and load transmission error of load 100Nm, see 3.
Example 2 The angle of the shaft is m=90. When the angle of the shaft angle is 001, the meshing path of the face gear tooth surface, the transmission error and the tooth surface load distribution with load of 100Nm and the bearing transmission are not considered when considering the edge contact and considering the edge contact. See error 4.
As can be seen from 3 and 4, a complete TCA and LTCA map is obtained when considering edge contact.
(1) At the edge contact point, the geometrical transmission error drops faster, indicating that the contact time of the two teeth at the edge contact point is very short, and the meshing of the conventional tooth surface or the engagement of the meshing is eliminated, so that it is received at the edge contact point. It is the effect of a momentary load, which can also be seen by the tooth surface load distribution map.
(2) Although it is theoretically possible to find the two edge contact points where the tooth tip edge of the face gear is in contact with the tooth surface of the small wheel, only one edge contact point actually has an instantaneous load during the load analysis.
(3) When there is a shaft angle error, the contact path is offset to the large end of the face gear, so the load distribution is also significantly offset on the tooth surface.
5 Conclusions (1) A simple calculation method for the contact between the tooth tip edge of the face gear and the small gear tooth surface is given, and the method for determining the principal curvature direction on the edge contact surface is given.
(2) Considering the edge contact and the LTCA under the condition of not considering the edge contact, the results show that the tooth surface load distribution has a certain difference compared with the bearing transmission error, which actually reflects the tooth tooth strength and dynamics after loading. Performance changes.
(3) Considering the bearing contact analysis of the face gear under the condition of edge contact, it is of great significance to improve the dynamic meshing performance of the face gear and design the high performance straight tooth surface gear transmission.